Paper Review - GHOST Protocol

Although I’m a big fan of Tom Cruise but this article is not about the movie from the Mission Impossible series. In this article, I discuss a paper by (Sompolinsky & Zohar, 2015) in which they introduce a protocol called the GHOST Protocol.

The paper presents an alternative called GHOST to Bitcoin’s Longest Chain selection rule for resolving forks in blockchain. This modification is proposed to allow increasing Bitcoin’s block creation rate without making it vulnerable to attacks.

Speed-Security Tradeoffs

In order for Bitcoin to be adopted as a global currency system, it must scale to support a high volume of transactions. In order to achieve this either block size or the block creation rate must be increased, both of which pose security tradeoffs in the form of vulnerability to various forms of attacks (e.g. double-spend attack, selfish-mining etc.) due to difficulty in the synchronization of the ledger between various nodes in time. ¹

Effect of Increasing Block Size

If the block size is increased, it will take longer for new blocks to be propagated throughout the network. The delay in propagation of new blocks is proportional to the size of the blocks (Decker & Wattenhofer, 2013). This delay could lead to increase in frequency of forks.

Effect of Increasing Rate of Block Creation

If the rate of block creation is increased, more blocks will keep getting created while the block was being propagated leading to forks. It should be noted that an adversary (assumed to be centralized) would not suffer from such a delay.

GHOST Selection

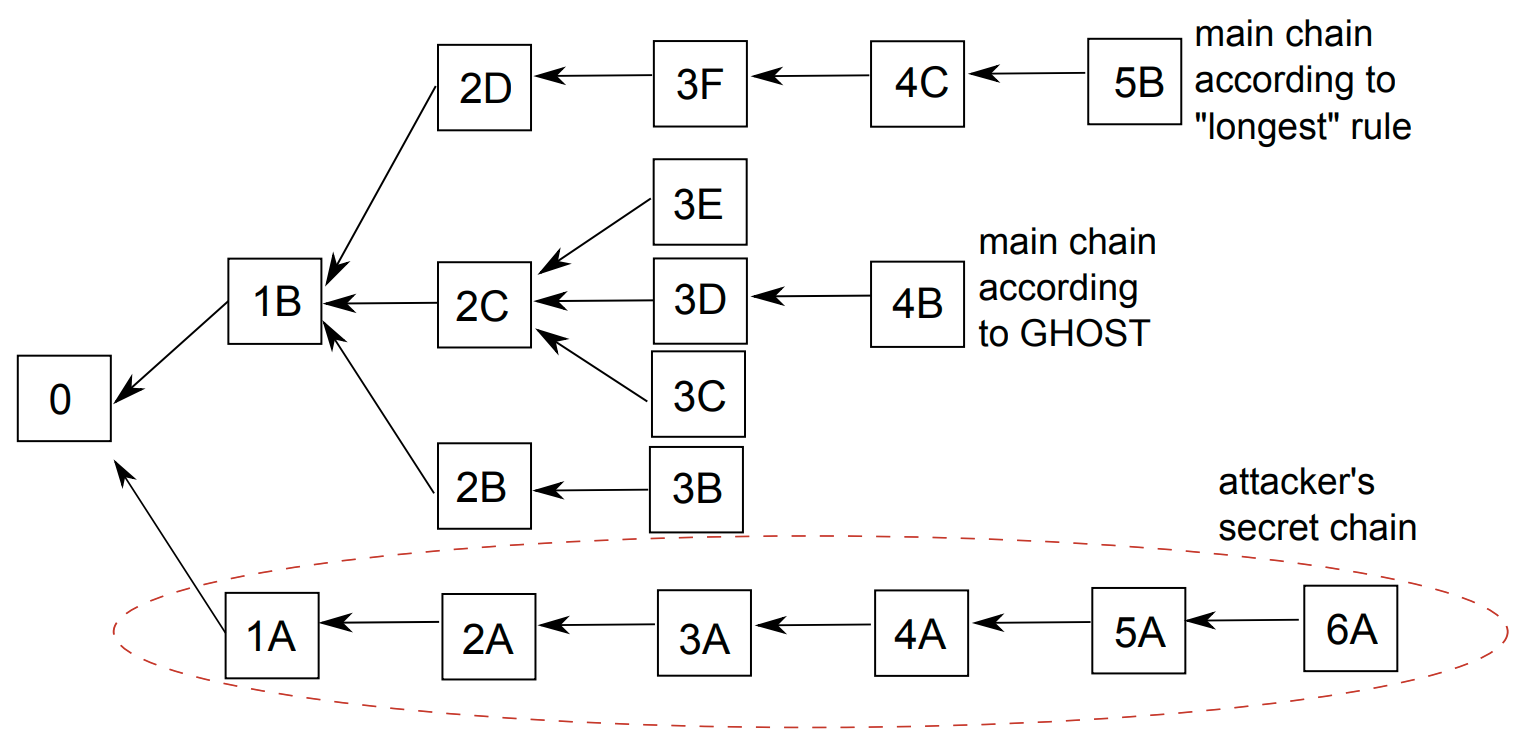
Consistency in Bitcoin is provided by the longest-chain rule which is based on the fact that the chain with the hardest Proof-of-Work should have been adopted by majority of the nodes in the system. This based on the principle that since the adversary cannot provide a harder Proof-of-Work than the honest network, the chain with the hardest Proof-of-Work must have been adopted by the honest nodes.

An adversary could take advantage of the delay in block propagation to present a longer chain that may not involve the hardest Proof-of-Work. Hence, the adversary will be able to attack the blockchain with fewer resources, reducing the security of the blockchain.

Greedy Heaviest-Observed Sub-Tree

Abbreviated as GHOST, extends this idea further to prevent wastage of PoWs of out of sync nodes by including them in the chain-selection rule.

GHOST Algorithm

Analysis of GHOST

Growth of Main Chain

Suppose $\alpha$ be the fraction of computational power in a subset of well-connected nodes. Let the delay diameter of the subset be $D$, the maximum time taken by a block from one node to reach another in the subset.

Longest Chain

With the longest chain rule the main chain grows with a rate of atleast $\beta_\lambda \geq \frac{\alpha\lambda}{1+\alpha\lambda D}$

GHOST

With the GHOST chain rule the main chain grows with a rate of atleast $\beta_\lambda \geq \frac{\alpha\lambda}{1+2\alpha\lambda D}$

Note that the growth is slower in GHOST because we have to wait for $D$ delay so that the new block gets propagated and no one creates block on other subtrees.

Upper Bound

Due to network delays the growth rate is limited in both GHOST and Longest Chain Rule. Let $S, T$ be two non-empty partitions of the network such that $\forall s \in S \text{and} \forall t \in T$ delay between $s$ and $t$ is atleast $d$ and let $P_S$ and $P_T$ be the fractions of computational power possessed in the partitions respectively. Then, $$\beta_\lambda \leq \frac{(P_S \lambda)^2 e^{P_S \lambda 2 d} - (P_T \lambda)^2 e^{P_T \lambda 2 d}}{(P_S \lambda) e^{P_S \lambda 2 d} - (P_T \lambda) e^{P_T \lambda 2 d}}$$

Security Threshold

Maximum fraction of resources possessed by the adversary relative to the honest network in order to have an exponentially high probability of a $51\%$ Attack.

Let the computational power of the adversary be $q\ \lambda_\text{honest}$ for some $q \in [0, 1)$.

Then, for longest-chain rule the security threshold is $\frac{\beta}{\lambda_\text{honest}}$ but for GHOST it remains constant at $1$. This is a consequence of the fact that forks still contribute to the weight of the subtree at an overall rate which the adversary can not match (while $q < 1$).²

Related Work

(Kiayias & Panagiotakos, 2016) introduce a new formal framework for the analysis of blockchain protocols that relies on trees (rather than chains) and also propose an attack on the Liveness property.

References

1. Sompolinsky, Y., & Zohar, A. (2015). Secure high-rate transaction processing in bitcoin. International Conference on Financial Cryptography and Data Security, 507–527.
2. Decker, C., & Wattenhofer, R. (2013). Information propagation in the Bitcoin network. IEEE P2P 2013 Proceedings, 1–10. https://doi.org/10.1109/P2P.2013.6688704
3. Kiayias, A., & Panagiotakos, G. (2016). On Trees, Chains and Fast Transactions in the Blockchain. Cryptology ePrint Archive, Report 2016/545.

Footnotes